

The elimination loop blindly divides by matrix((x - 1), (x - 1)) which very well could be 0.
#Freemat diagonal of matrix code
Is there anything I can do to make this code better? Sol = (matrix(i, x) - counter) / matrix(i, i) Matrix(j, k) -= matrix(i, k) * matrix(j, i) / matrix(i, i) I used indent -kr -i8 -l1000 -lc1000 for styling and I used preprocessor for simplifying the matrix math but some pieces make no sense as as matrix(x, -2): # include # include # define matrix(i,j) matrix int gauss ( double *matrix, int x, double *sol) ĭouble *mat = malloc((x + 1) * x * sizeof( double)), *sol = ( malloc(x * sizeof( double)))
#Freemat diagonal of matrix how to
I used linear matrix because I simply don’t know how to declare multidimensional array with malloc and I don’t know how to pass it as a parameter to function. I was wondering what I can do to make the code shorter (keeping the good style), with better performance and with better memory consumption. Sol= matrix/matrix įor( int j=x -1 j>i j-) counter+= matrix *sol
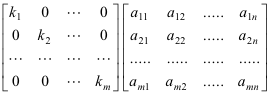
# include # include int gauss ( double* matrix, int x, double* sol) ĭouble *mat = malloc((x+ 1)*x* sizeof( double)), *sol =( malloc(x* sizeof( double))) a pointer to the matrix of coefficients.Also give the algebraic multiplicity of each eigenvalue. Find Eigenvalues and their Algebraic and Geometric Multiplicitiesįind the eigenvalues of the matrix $A$. Suppose the following information is known about a $3\times 3$ matrix $A$. Determine Eigenvalues, Eigenvectors, Diagonalizable From a Partial Information of a Matrix.(b) Find the dimension of the eigenspace $E_2$ corresponding to the eigenvalue Let $A$ be an $n\times n$ matrix with the characteristic polynomialĪssume that the matrix $A$ is diagonalizable. Determine Dimensions of Eigenspaces From Characteristic Polynomial of Diagonalizable Matrix.The red graph is for $A$, the blue one for $B$, and the green one for $C$.įrom this information, determine the rank of the matrices $A, B,$ and The graphs of characteristic polynomials of $A, B, C$ are shown below. Let $A, B, C$ are $2\times 2$ diagonalizable matrices. Given Graphs of Characteristic Polynomial of Diagonalizable Matrices, Determine the Rank of Matrices.Your score of this problem is equal to that Find the dimension of the null space of the matrix $A-aI$, where $I$ is the $3\times 3$ identity matrix. Maximize the Dimension of the Null Space of $A-aI$.The zero matrix is a diagonal matrix, and thus it is diagonalizable. Is every diagonalizable matrix invertible? Every Diagonalizable Matrix is Invertible For each eigenvalue $\lambda$ of $A$, find a basis of the eigenspace $E_įor this problem, you may use the fact that both matrices have the same characteristic.Find eigenvalues $\lambda$ of the matrix $A$ and their algebraic multiplicities from the characteristic polynomial $p(t)$.Find the characteristic polynomial $p(t)$ of $A$.Let $A$ be the $n\times n$ matrix that you want to diagonalize (if possible).
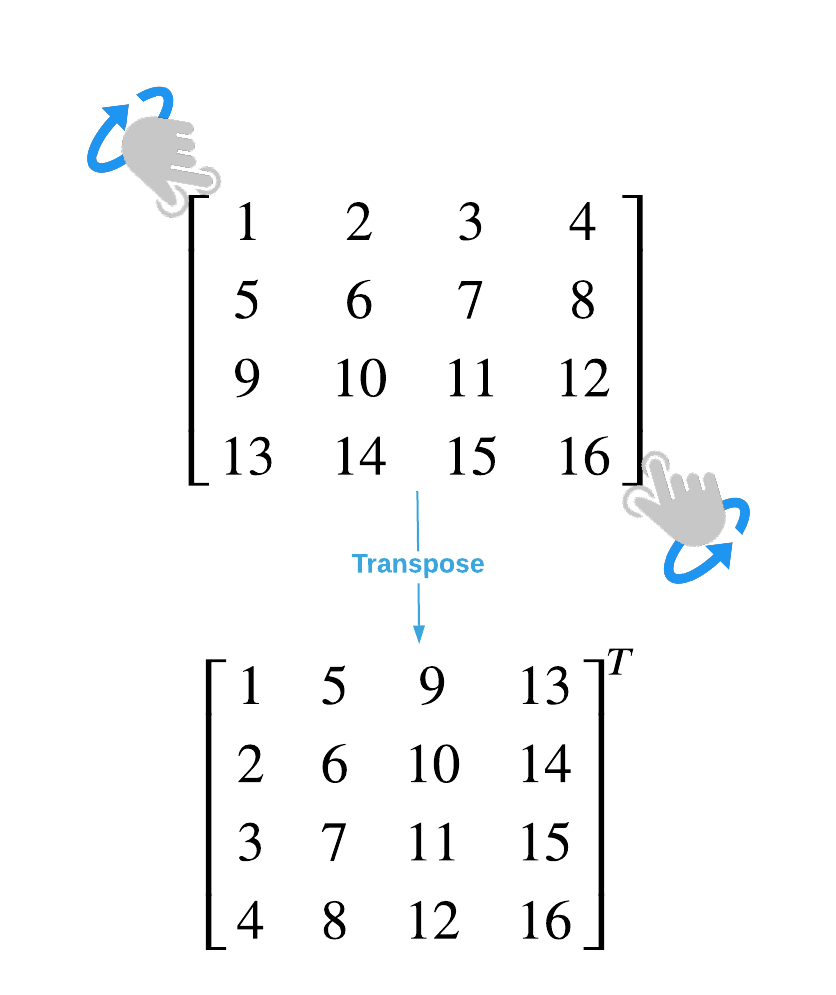
A concrete example is provided below, and several exercise problems are presented at the end of the post. The process can be summarized as follows. We only describe the procedure of diagonalization, and no justification will be given. Here we explain how to diagonalize a matrix.


 0 kommentar(er)
0 kommentar(er)
